Math Quiz

Just a few questions to check your math skills.

1-24. Calculate the factorial of 7.

(A) 28
(B) 720
(C) 5,040
(D) 40,320

[popup type=”” link_text=”Answer” link_class=”button”] (C) 5,040 [/popup]

[popup type=”” link_text=”Discussion” link_class=”button”] A factorial, commonly denoted with an “!” or in this problem would be 7!, is the product of an integer and all the integers below it to one. For example, 4! = 4 × 3 × 2 ×1 = 24.

This for this problem the answer is 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5,040. [/popup]

---

1-25. Using Pascal’s triangle allows one to determine which terms of the binomial expansion?

(A) coefficients
(B) exponents
(C) higher order terms
(D) permutations

[popup type=”” link_text=”Answer” link_class=”button”] (A) coefficients [/popup]

[popup type=”” link_text=”Discussion” link_class=”button”] Knowing how to quickly construct Pascal’s triangle allows you to quickly determine the coefficients for a binomial expansion.

The binomial expansion is a mathematical theorem that specifies the expansion (multiplying out…) of any power (a + b)^m of a binomial (a + b) as a specific sum of products aⁱb^j. For example,

$$ {{\left( a+b \right)}^{2}}={{a}^{2}}{{b}^{0}}+2{{a}^{1}}{{b}^{1}}+{{a}^{0}}{{b}^{2}}$$

recall that something raised to the 0 power is equal to 1. Also, the coefficients for the resulting three terms are 1, 2, and 1. There are m+1 terms and m+1 corresponding coefficients in the expanded form.

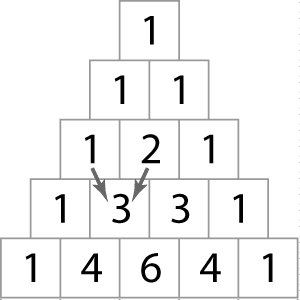
Pascal’s triangle is a triangular array with 1’s at the ends of each row (1 at the apex or first row, too) and of the other values in a row is the sum of the two numbers in the row above.

The two arrows point to the first 3 on the forth row, which is the sum of 1 and 2 found on the row above.

The coefficients for the expansion of (a + b)² above are the values in the third row, 1, 2, and 1. For (a + b)³ the coefficients are 1, 3, 3, 1 as found in the forth row. The binomial expansion for (a + b)³ becomes

$$ {{\left( a+b \right)}^{3}}={{a}^{3}}+3ab+3ab+{{b}^{3}}$$ [/popup]

---

1-56. Identify which the following Boolean algebra expressions is correct.

(A) 1 + 0 = 1
(B) 1 + 1 = 2
(C) 1 − 0 = 0
(D) 1 − 1 = 0

[popup type=”” link_text=”Answer” link_class=”button”] (A) 1 + 0 = 1 [/popup]

[popup type=”” link_text=”Discussion” link_class=”button”] Recall your Boolean truth table for A or B (A + B)

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 1

Boolean values include only zero’s or one’s. Thus response (B) is common base 10 integer addition. The minus sign is a way to convening the “not” logic element making 1 – 0 = 1 + 1, which is equal to 1, and 1 – 1 = 1 + 0 which is also equal to 1.[/popup]