
Down to the last week of preparation for the exam on March 2nd. Good luck to all those signed up for that exam date. Time to focus on preparing your notes, organizing your references and doing a final run through of practice exams.
A common formula that you should pretty much just know by heart, for the exam is the exponential distribution’s reliability function. Remembering ‘e to the negative lambda t’ or ‘e to the negative t over theta’ will save you time during the exam.
$$ \large\displaystyle R\left( t \right)={{e}^{-\lambda t}}={{e}^{-{}^{t}\!\!\diagup\!\!{}_{\theta }\;}}$$
R(t) is the reliability or probability of success at time t.
t is time or miles or pages printed, etc.
λ is lambda and the failure rate per unit time.
θ is often called MTTF or MTBF (see NoMTBF.com for issues with this four letter acronym).
Note that 1/λ = θ, which is a useful fact to remember for this distribution.
Let’s explore an example question that requires the knowledge above to solve.
What is the reliability of the following system at 1000 hours, assuming all components have constant failure rates?
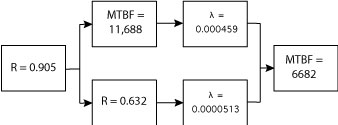
(note: not sure how the lower edge of some boxes got clipped. Still learning how to use Illustrator.)
As you can see, there is a mix of reliability, MTBF (θ), and failure rate (λ) information in the reliability block diagram, RBD. The first step is to convert the MTBF and failure rate values to reliability.
For the MTBF use
$$ \large\displaystyle R\left( t \right)={{e}^{-{}^{t}\!\!\diagup\!\!{}_{\theta }\;}}$$
to convert the two MTBF values to reliability. Then use
$$ \large\displaystyle R\left( t \right)={{e}^{-\lambda t}}$$
to convert the two failure rate values to reliability. Remember that in this example time, t, is 1,000. The results are
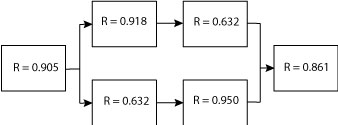
The next step is not really related to exponential distribution yet is a feature of using reliability and RBDs. We can simplify this reliability block diagram by solving for the two elements in series, which are also in parallel (R = 0.918 and R = 0.632). For elements in series, it is just the product of the reliability values. The same applies to the two other blocks in series also in parallel (R = 0.632 and R = 0.950).
The results are
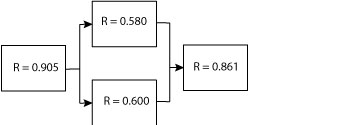
Next we need to reduce the two elements in parallel to one block, which creates a simple series system overall. For the two in parallel, keep in mind that the one minus the product of the unreliability values results in the reliability of the elements in parallel.
$$ \large\displaystyle R\left( t \right)=1-\left( 1-{{R}_{1}}\left( t \right) \right)\left( 1-{{R}_{2}}\left( t \right) \right)$$
Using (R = 0.580) for R1 and (R = 0.600) for R2, we find that reduces to R = 0.832.
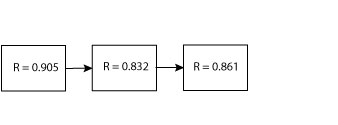
Now the problem is a simple RBD with three elements in series. The product of these three reliability values is 0.648.
We found that during the preparation course the exponential reliability functions continued to appear over and over in the sample problems. Be prepared and know these key formulas and concepts.
Related:
Common formulas (article)
Using The Exponential Distribution Reliability Function (article)
The Exponential Distribution (article)
Thanks again for taking time to do these sessions. Extremely helpful.
You are very welcome.
Very detailed and comprehensive. Thanks a lot.
Do you have an article on how did this reliability equation come about? What is the science behind the equation: r(t) = e^(-t * lambda)?
Hi Jeremy,
Good question, I do not think we have an article on the origin of the exponential equation – it’s a good idea to see what we can find. The Weibull distribution has a nice story, maybe share that one as well. Guess this is an idea for a series of articles – thanks!
Cheers,
Fred
Great articles, as a reliability advisor with a major global integrated energy company, these articles help me better articulate them to the ops and projects I support.
One minor pedantic point; MTBF and MTTF are not acronyms, they are abbreviations ?.
An acronym is an abbreviation using the first letters of each word.
What would be best acceptable R value for a complex system to be guaranteed for it’s mission duration over and over again
Hi Azeem,
the short answer is set R to whatever you want and see how it goes. The reliability of the system will be what it is – separate from what you want it to be. A suitable reliability value depends on the technology capability, customer expectation, cost of maintenance or replacement, etc.
Some very complex systems have very, very high availability, yet rather low reliability – they also are designed to continue to run even is elements within the system fail and repairs can occur as the system operates. Other systems are very available and reliability and maintenance costs are very low… again, it always depends on what can do, what you can afford to do, business factors, and market factors.
If the system is existing – you may have some data to sort out the reliability of the system and do some calculations on costs, etc to determine if that is good enough or not.
cheers,
Fred
Fred,
Brilliant, response thanks. In building dependable systems what matters is how to determine an assurance number that can deterministically accounts failure risk parameter in a system consisting of different elements, components, products, services including, materials, communications, information, non-material systems, subsystems and it’s associated sets & subsets including the human factor.
Are there any models available similar to Systems Engineering backbone to plug the inputs and get the minimum threshold dependability factor to verify the functional applicability and it’s range. It’s all narrows down to the requirements, specifications and designs those are changing so fast that hardly any time tested component, element, material, services available to use for the novel type design demands. In this case how can the compliance and assurance is maintained for any system delivered against any code or standard. With the present technology we can only do a system test against it’s base line design or some destructive tests but it will not reveal how the system evolves to fail. Which implies that no means available to create an unknow faults to test the system behavior which finally leaves to natural selection process and what ever we do the fault cannot be eliminated and an unknow failure do occurs every time in the system then fix it then next new failure occurs then fix it so on so forth.. .this phenomenon is seen in almost a facets , some times deliberately for business gains.
Excellent presentation of the theory of weakest link – it would be interesting to see how actual equipment holds up in a physical test. That is what I am interested in.
Thanks for the articles.