Finding and eliminating early life failures
MTBF for electronics life entitlement measurements is a meaningless term. It says nothing about the distribution of failures or the cause of failures and is only valid for a constant failure rate, which almost never occurs in the real world. It is a term that should be eliminated along with reliability predictions of electronics systems with no moving parts.
There is also another term widely used in reliability engineering that is a bit of a misnomer and should be eliminated, that is the term “Infant Mortality”. The term “infant mortality” typically is used to describe early life failures in an electronics system during the declining hazard rate period which may extend to its technological obsolescence.
It is my experience that it is a term used dismissively as it if it was “expected” or acceptable as a intrinsic yet generic cause of failures within the first weeks or months of a new product introduction. It is also considered by some traditional reliability engineers I have met as a “quality department” problem, not to be confused with reliability engineering.
The vast majority of human infant mortality occurs in poorer third world countries and the main cause is dehydration from diarrhea which is a preventable disease. There are many other factors which contribute to the rate of infant deaths, such as limit access to health services, education of the mother, and access to clean drinking water contribute.
Human infant mortality is defined as the number of deaths in the first year of life. The contributing causes of human infants and failure of electronics of course are completely different. Causes of human infant mortality comes from the fact that at birth a child may go through a complicated delivery and does not have a fully developed immune system, so it has less resistance to infections. The lack of health care facilities or skilled health workers is a contributing factor.
An electronic component or system is not weaker when fabricated; instead it has the highest inherent strength when turned on for the first time. Opposite of humans, electronics are “adult” when first produced and decline in strength (fatigue life) from that point on. This is why we can subject new systems to high levels of environmental stress to remove latent defects (HASS process) without taking significant life from it.
So why use the dismissive term “infant mortality” to describe latent defects in electronics as if they are expected? The time period that we would classify as “infant mortality” in electronics is arbitrary. It could be the first 30 days or the first 18 months or longer. Since the vast majority of latent (hidden) defects that are found early come from mistakes and errors either in design or manufacturing and is therefore not controlled, they can have a wide distribution of times to failure. Many times the same mechanism in which the weakest manifestations may occur within 30 to 90 days continues as declining rate through a products useable life period.
Failures of electronics systems in the first days or months after manufacture are not due to intrinsic wear out mechanisms that are known. We can only model those failure mechanisms that have an intrinsic and repeatable physics of failure.
Traditional reliability engineering has been focused on making predictions of the life entitlement of electronics systems using cookbooks of FIT rates to derive a system MTBF or MTTR. This is in spite of the fact that there is little or no evidence of empirical correlation to actual causes of most electronics failures. Traditional reliability engineering it seems has not been very focused on early discovery of the causes of early life failures during the the declining hazard rate after market release. Semantics is important and carries implications. The term “infant mortality” contributes to dismissing the significance of early life failures to the overall reliability of a system. Yet, it is where the vast majority of costs are for the customer and any electronics systems manufacturer.
Because electronics are not “infants” and not weaker when first “born” we can be aggressive in our treatment of them before they leave the “birth room”. Unlike newborns we can put new electronics through a stress test and if they fail diagnose and discover an assignable cause which then we can correct for and prevent further failures. Through HALT and HASS we can find the root causes of latent defect failures and by removing those from the production population eliminate the most costly time period of defects and failures which because of the potential wide time distributions can extended until the product is replaced due to technological obsolescence. I believe the term infant mortality when applied to electronics has the connotation that it is expected, inherent, unavoidable, and due to nature. It should be used for human life cycles, not electronics life cycles.
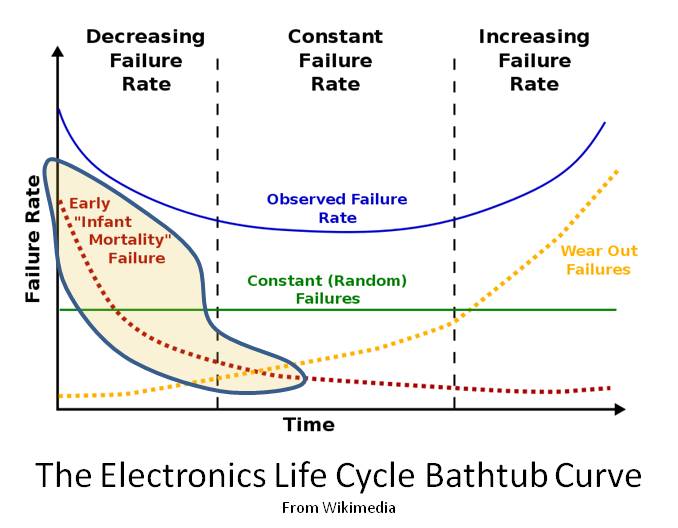
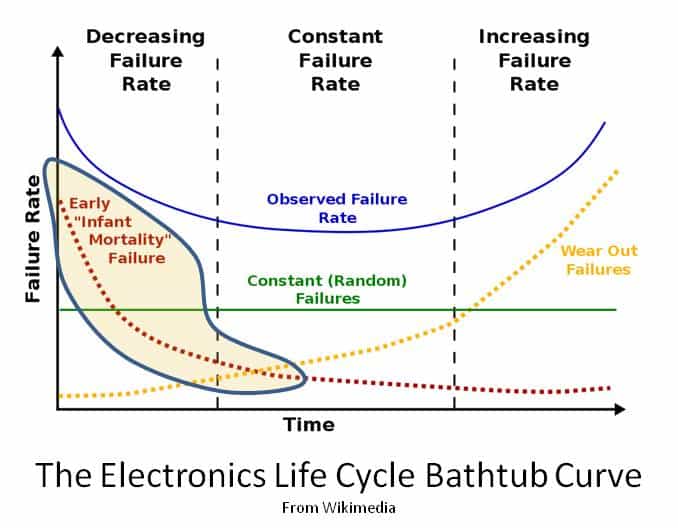
The chart shown has a “typo.” The vertical axis should be Hazard Rate, not Failure Rate for the “bathtub curve.” This is not just academic: the integral from 0 to infinity of the Failure Rate is 1, the integral for the Hazard Rate is unbounded.
Infant mortalities in electronics are often quality problems in component manufacturing, or in shipping, handling, and storage of components before or during higher level assembly. Shipping, storage, and installation of the top level product can also produce infant mortality failures.
These infant mortalities are almost always caused by some event damaging the component and causing a stress concentrator. This can be as innocent as a scratch or nick that starts a high speed version of what is normally a wear-out failure mode. For instance, an ElectroStatic Discharge (ESD) event can often damage an IC internally, thinning the metallization, which causes high current density and electromigration at that location which takes weeks not years to completely open circuit the damaged internal trace.
True, infant mortalities do continue forever, but they are usually less important than random-in-time and wear-out failures after a few months. Some companies consider a failure a quality problem if it occurs in the first month. Most companies use three months as their arbitrary cutoff time.
Thanks Chet. The bathtub curve graph image and axis labels were copied directly from Wikipedia. I did not catch their misuse of failure rate versus hazard rate in the graph.
@ Kirk
You raise a good point about the use of the “dismissive” term infant mortality and that it is often used to explain an early life failure is “OK” because we somehow “expected” it. Unfortunately we miss the opportunity to improve when we justify a failure as acceptable for such a capricious reason.
I also agree we need to eliminate the use of the term “infant mortality.” It’s actually a pretty insensitive term to describe early life failures of engineered systems.
@ Chet
I’m curious how you are defining failure rate. From your statement, you seem to be referring to the probability density function (pdf). In my experience, failure rate is engineering vernacular for hazard rate. This is typical in texts on the subject of reliability. Just curious because if you are referring to the pdf, your statement that the integral over the domain [0, inf) is equal to one isn’t generally correct.
Hi Andrew:
You are correct. I am referring to the pdf (probability density function) as the Failure Rate. It is the “histogram” of when failures occur. The integral from 0 to infinity of the pdf is the CDF (cumulative Distribution Function), which is a probability that equals 0 at time = 0, and approaches 1 as time approaches infinity.
Andrew and Kirk,
If you use the exponential model, then 1/MTBF IS the “failure rate,” and it is constant and is coincidentally the “hazard rate” for the exponential model. This is the common usage of the term from a 217 perspective, but only applies for the exponential model.
Chet is indeed correct, the y axis should be labelled “Hazard Rate.”
Another big issue with the chart is that it is very commonly misinterpreted, and Chet hinted at it in his last paragraph. Many folks who see this “bathtub curve” believe that once the infant mortality failures have happened that the hazard rate changes to a constant, and then as more failures occur to an early wearout hazard rate, and then eventually as even more failures occur to an old age hazard rate. Nothing can be further from the truth if the product’s design and manufacturing processes do not change. The hazard rate is only determined by the failure distribution, which cannot change unless the product’s design or manufacturing processess change.
Mark Powell
Mark
You hit the nail on the head with “many people see” the bath tub curve is a simple model of a generic system. It can help in thinking about how things “fail” and hence what can be done to prevent failure, but it is not real life.
Hi Richard,
Thanks for the comment and support. Even with humans the bathtub curve is a mixture of many different failure mechanisms.
cheers,
Fred