
Received a sample problem from someone preparing for the CRE exam saying it was a tricky one.
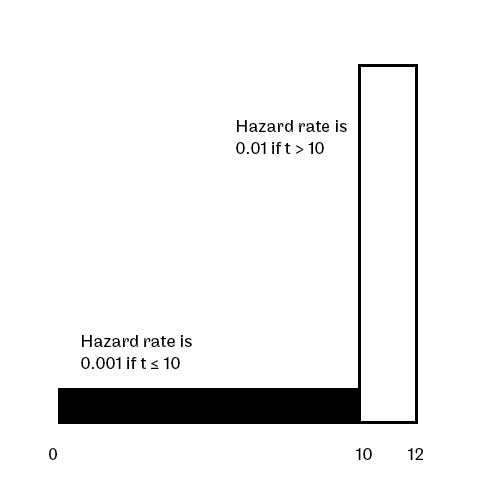
The hazard rate function for a device is given by
0.001 if t ≤ 10 hours and 0.01 if t > 10 hours
What is the reliability of this device at 12 hours?
I first draw the hazard function
Recall that the area of the box is the probability of failure. Thus we can multiply the duration and corresponding hazard rate to find the probability of failure.
0.001 × 10 = 0.01 probability of failure over the ten hours, and
0.01 × 2 = 0.02 probability of failure over the remaining two hours.
Convert to reliability by recalling that the 1 – probability of failure = reliability. The CDF is the compliment of Reliability, 1- F(t) = R(t). This results in the reliability over the first ten hours of 0.99, and over the next two hours as 0.98.
Now multiply the two to get the reliability over 12 hours, 0.99 × 0.98 = 0.9702. Therefore the answer is A.
How about those other possible answers.
B is just the reliability of the last two hours 1 – (0.01 × 2) = 0.98
C is all twelve hours at the lower hazard rate, 1 – (0.001 × 12) = 0.988
D is just the reliability of the first 1en hours 1 – (0.001 × 10) = 0.99
Thoughts? Is there a better way to solve this one?
Related:
Hazard to Reliability Functions (article)
The Exponential Distribution (article)
Reliability Function (article)
One way to think about this: if R(t) = exp{- integral from 0 to t of h(t)dt} the integral can be simply computed from the area of the curves as 10*(0.001)+2*(0.01) or 0.03. This results in R(t) = exp(-0.03) or 0.9704.
Excellent thanks Steve
R(@ t=12) = R(@ t=10) x R(@ t=2)
R(@ t=10) = e^(-0.01) = 0.990
R(@ t=2) = e^(-0.02) = 0.980
R(@ t=12) = 0.990 x 0.980 = 0.970
Hi Spyros – using the exponential reliability function. That worked in this case yet I caution it may not work in other cases where the hazard or probability density function are provided.
While the exponential reliability function is useful, it really only works when the PDF also is exponential.
Cheers,
Fred